Fibonacci Numerals
This post is for my notes on what I am calling the Fibonacci Numeral system. First I will go over numeral systems and how they were used.
Roman - (Abacists) consisting of letters I, V, X, L, C, D, M and designed for fast calculations using a bead frame or other device. No (0), or (-).
See How Did the Romans Calculate? | blog@CACM | Communications of the ACM
https://cacm.acm.org/blogs/blog-cacm/234881-how-did-the-romans-calculate/fulltextThe Abacus is an intuitive way of learning math, simpler than our base 10 system. It does run into trouble with less intuitive operations - division, powers, and extremely large numbers; the same areas our intuition fails. With regard to large numbers - the myriad, (X̅ i.e. 10,000) seems to be the largest number that we have some sense for and is not quite a complete abstraction.
Arabian - (Algebraists) numbers 1-9 and place values. (0) and (-) included. Calculations are done with paper and pencil using an algorithmic system*. It has the advantage that the calculating system and the writing system are integrated together. The best algorithms for this are the ones taught pre-common core. The idea with common core education is that learning the ideas is important but being able to do it well and quickly is not, so you get horrendous but more accessible algorithms like drawing lines, putting dots at intersections and counting them. With carefully selected numbers this can be easy and look smooth, but with less carefully selected numbers it blows up fast.
*(Technically the methods to use an abacus are also algorithms, and you can also learn to do it quickly and in your head with practice see mental abacus.)
Arabic but with other bases - this uses another number than 10 as the base, common ones are 8,12, 16, 20, 60. Base 2 (binary) is technically of this type but is used differently enough in practice that I would consider it its own thing. Binary efficiently stores information but is incompatible to the way we think and do things. These alternate bases usually go for binary compatibility or for having lots of natural fractions. Bases 8 and 16 easily convert into binary, with each digit (octit? hextuplet?) taking 3 or 4 spots in a binary string. Bases 12, 20, and 60 divides easily into the common divisions - halfs, thirds, fourths, &c. 60 is divided evenly by 5, 6, 10, and 12. That is why the Babylonians picked it and why we have 60 minutes in an hour. The fifth of an hour is pretty neglected.
Scientific Notation - This is an elaboration of the Arabic numerals stemming from realizing that the precision inherent in a number more than a thousandth part is usually not needed and is almost always unjustified. If I wanted to say how many troops were in a military theater, for example, saying the first two numerals convey the information adequately and the rest add little for most purposes, and is difficult to get exactly right. Saying 620k troops invaded Iraq gets the relevant information across. 617,821 adds little that is of use for almost every application and is almost certainly wrong. You write the significant digits and then their place value after the letter ‘e’. 6.2e5
Other numeral systems: - I toyed with one when younger based on squares, because squares have some unusual properties - learning squares and some of these properties makes it possible to derive the rest of the multiplication table with only a little addition and subtraction instead of having to memorize the whole thing. Also, the squares would naturally increase in size as the numbers worked with got bigger giving some of the advantages of the scientific notation. Eventually I abandoned it as you would have to have some hard boundary or keep introducing numerals without end. And the multiplication trick also adds more and more adjusting additions as the numbers get bigger, so it loses its utility.
Fibonacci Numerals
The system I present here borrows intuitive inherent addition from the abacist systems, and place value from Algebraist system.
The numbers in the Fibonacci sequence are numerals, and other numbers are represented as sums of those numerals. The Fibonacci sequence is 0,1,1,2,3,5,8,13,21,34,55,89,144… every number is the sum of the two numbers before it.
In this system If I wanted to write six, which is not on the sequence, I would write 5+1. I could do this Roman Numeral style, 51 meaning 5+1.
Counting this way gives us: 1, 2, 3, 3+1, 5, 5+1, 5+2, 8, 8+1, 8+2, 8+3, 8+3+1, 13…
Addition follows simple rules, like checkers. When there are 2 numerals in sequence the smaller jumps the greater to form the next numeral. A negative next to positive leads to the larger jumping the smaller. A negative and positive at the same numeral cancels each other out. That’s it - that covers all addition and subtraction.
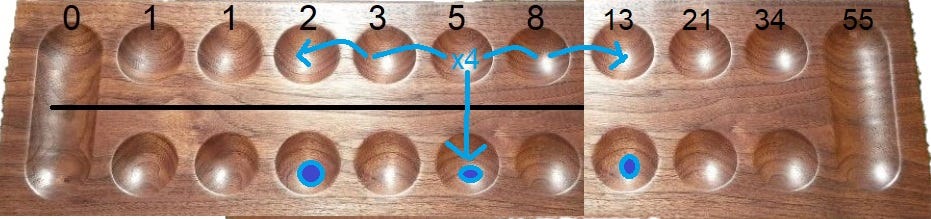
In order to visualize this better, imagine a counter with depressions built into it for each numeral, something like a mancala board.
Each spot has a value, following the Fibonacci sequence. A bead in the one spot to represent the number one. Another in the 8 spot represents the number 8. Together they represent 9.
Two beads together leads to a jump: if both positive the lower jumps up. If mixed the higher jumps down.
To subtract 5 from our 9 (8+1) above, you put a negative bead (say the color red) in the five spot. The bead at eight is next to it, so it would jump the five into the three slot, the bead at one is untouched, so your answer is 1+3, and you write 31. Or whatever symbols are actually used for this.
The beauty of this is it remains just as simple as the numbers become larger and if you have a bead at 89 and a bead at 144 you would jump to the next slot, which would be 233.
A negative and positive bead with a slot between them leads to the large moving down one slot, and the smaller being removed.
If you end up with two or more beads in the same slot you can work it by simply reversing the sequence and making one bead turn into two beads in the previous two spots.
For example, if we have two beads in the five slot (5+5), we take a bead out of 5 and put beads into the 2 and 3 slots. Then we have the 3 jump the five into the eight slot. Answer is 2 and 8. Adding identical numbers this is the same pattern for any number and makes for a simple x2 rule. More on multiplication in a following section.
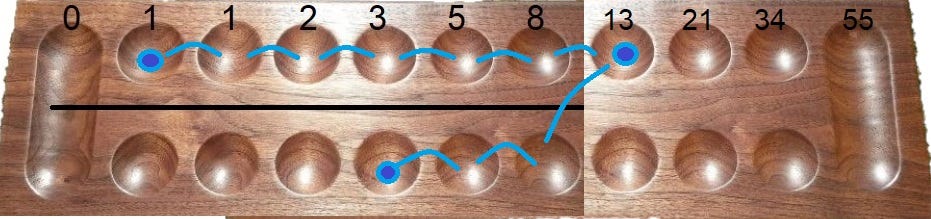
This same technique is used to subtract numbers that aren’t close to each other. Lets say we are subtracting 3 from 13. We place a blue bead at 13 and a red bead at 3. 13 turns into 8 and 5. 5 is next to the -3, so it jumps it and becomes two. Answer is 2 and 8. 55 - 13 would follow the same procedure, just shifted over on the counter 3 slots so 8 and 34.
How do you keep the total number of numerals bounded?
The Fibonacci sequence is infinite so there would be an infinite number of numerals, which makes the whole thing clunkier and clunkier to use as the numbers get larger.
To prevent this, we cap it at ten numerals which are: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. 0 is a special case so we have 11 numerals, one more than the Arabic system. The next Fibonacci number is 144 so to represent it we use place value as in the Arabic system. It is ‘1’ but with some indicator that it is in the next set in the series. In a way this part of it is a base 144 system. It is also a powers system, with the ratio between adjacent numerals approaching 1.62, meaning the ration between any numerals is some power of 1.62 (approximately). 21-55 is approximately 1.62^2 because there are two steps between them.
Multiplication Patterns
Multiplication follows a pattern for every number no matter what it being multiplied. For numbers with lots of beads there is a lot to keep track off, but the basic patterns for up to 10x are simple.
Times Two: 1 bead up and 1 bead two down as we saw above.
2x8 = 13&3. 13 is one up from 8, and two down from 8→5→3. You would do this with every bead when multiplying by 2.
Times Three: simply add another bead to the original slot which then jumps the 1 bead up. Rule is 1 bead up two, 1 bead down two
. 3x8 = (2x8) + 8 => (3+ 13) + 8 => 21+3.
Times Four: Same as the times three pattern, just add another bead in the original place.
4x8=21+8+3. And this is pretty clearly 3x8 with an additional eight. It doesn’t matter what you are multiplying by 4 the pattern holds, for example, 4x5.
I’ll write out the patterns for the rest with the strikethrough being the original place:
x5=x00x000x
x6=x0000x0x
x7=x0000000x
x8=x000x000x
x9=x0x00x00x
x10=x0x000x0x
x11=x0x0x0x0x
x12=x00x0x00000x
Some multiplications turn out to be easy because of the structure of the number system (such as x7 for this one, instead of x5 for our base 10 system). Memorizing a single pattern for each one is simpler than memorizing the times table. Multiplying numbers with multiple numerals will get messy, but this is also the case for us when we are multiplying numbers with two or more digits.
The Counter Edge
These patterns lead to a problem with the left edge of the counter. What happens when you get to 0, but according to the pattern you should keep going. The answer is working out the Fibonacci sequence to the left which means subtracting the two numbers to the right to get the previous number in the sequence. ? 0 1 1 2 3 5… ? is 1 - 0 or 1. Doing this a few times gives us …5 -3 2 -1 1 0 1 1 2 3 5… . We see the left side of the sequence is the same as the right, just with every other number being negative. When we are moving onto the edge on the counter the bead ‘bounces’ back when it hits zero and just flips sign with every step after that.
Let’s demonstrate with 7x2.
Now lets go left one more to flip to negative on the last step. Let’s do 7x1. Using beads with different colors on the sides would be handy so after the bounce you can flip it over with each step.
1x7 = 8 - 1. So far, we have only worked with positive numerals. Some versions of Roman numerals allow you to subtract numbers from the main number i.e. for 9 you write IX (10-1) instead of VIIII (5+1+1+1+1). This is the conversational equivalent of saying it’s a quarter ‘til one instead of twelve fourty-five. We can use the convention for our system that when the smaller numeral is before the larger, it is negative.
Negative Numerals
The use of negative numerals introduces the problem that there are many different ways to write the same number. 7 could be written as 8-1 or could be written as 5+2. There should be one standard way to write a number, and a simple rule to determine how they should be written.
We could use the human intuition of quarter ‘til the hour. The rule here seems to be if its pretty close we bump up to the next big unit of the hour. Twenty ‘til is the border case where it starts sounding odd. Saying 25 ‘til or a half hour ‘til is definitely odd. Since we are using numerals with the ratio phi (.62) built in the obvious rule is you use the negative if the distance to the next numeral is less than 1-phi than to the previous numeral. More simply stated, you want to keep the small numerals as small as possible. Thus 8-1 is preferred to 5+2, because 1<2. 3+1 is preferred to 5-1, because the 1 in 5-1 is not larger than the 1 in 3+1. Other examples:
8+2 not 13-3
13-2 not 8+3
13+3+1 not 21-(3+1) or 21 - (5-1)
In our counter system the rule that is being followed is that if you have the pattern xox you replace it with -x00x. And additional rule for approaching this from the other direction is -n--x > x--x- (n is negative). These two rules assure a uniform way to express a number and that the number of numerals is minimized, and that 55-10 has 10 in a consistent form (55-(8+2)) instead of something like 55-(13-3)
3+1 is understood to have the leftmost 1, not the second 1 slot. 3+1 gives trouble in several places so we need a rule for 17, 72, 106, 127. That rule is if you have 21, 3, and 1 together they have to all be the same sign positive or negative. If not, replace with 13, 3, 1 all with the same sign.
Applying this rule to our multiplication patterns simplifies some of them
x4=x0x0x=>(-x)000xx=>(-x)00000x Now the pattern has two beads instead of three.
Compare to 4x8 given above.
x10=x0x000x0x=>(-x)000x00x0x
x11=x0x0x0x0x=>(-x)000xx0x0x=>(-x)000000000x
It would be nice if the multiplication patterns tended to give you the correct negatives without need for further adjustment. In the 1x7 pattern we used above we find that if we use the second 1s slot for our multiplication we get 8-1 while using the first 1s slot gives us 5+2. Using 1x8 in the first 1s slot gives us 1+2+5 which consolidates to 8, whereas doing it in the second 1s slot gives us simply 8. 1x12 give us 13-1 not 8+3+1 regardless of which 1s slot is used. There isn’t a simple way to get the results already corrected, they have to be checked. I’m assume with use these rules would become second nature, and the alternate ways of saying numbers would just sound wrong, like poor grammar.
Division
For division we reverse engineer multiplication patterns. To divide by 2 we take the multiply pattern and reverse it. x*2 is x00x, so we look at the largest numeral of a number see if there is a bead three slots to the left. If so, we remove both beads and place a bead one slot to the left on the quotient row. If not we place the bead in the quotient row one slot over and a negative bead three slots over. The negative bead and any other beads remaining in the dividend row and must be worked. If the beads in the dividend row are equal to the divisor it is just moved to a 1 slot on the quotient row. Any beads that are less than the divisor are the remainder, and we are done (assuming no jumping or simplification needs to be done.) During these operations we can jump and Un jump beads, place matching negative-postive pairs in order to create the divisors patterns.
More practically - you take the right most numeral of your number, use the divisors pattern to determine the first quotient numeral, and put the remaining beads in the divisors pattern in place, with sign flipped. Here is 13 divided by 4:
The pattern for 4 is (-x)00000x. We remove the rightmost bead, place one in the quotient row for the centerplate of the pattern and complete the action by placing the other xs in the pattern with signs flipped: the (-x)→x in the ones place. The answer is 3 Remainder 1. If there had been more beads in the dividend larger than 4, we would apply the process again to any bead representing a value larger than 4.
This does create the problem of what to do when the divisor is large, or fractional and not the smaller memorized pattern. In these cases you will need to use something like the Algebraist algorithm, which is guesswork, multiply to check your guess, and do lots of calculating. The nice thing is that you can carry negative numbers and back work with them. Calculate say 100/12.7 with the algebraist method to see that it is as crazy as I’m saying - look at the leading numbers and their place value to start your first guess, and there will be lots of calculating involved.
Fractional (Decimal)
To be worked out. Decimal is a standard fractional system for is. It is just an infinite summed series of fractions of power of 10 to represent all fractions, which works well in the arabic system. In practice you don’t go infinite with them, just go as far as reasonable.
For Fibonacci numerals there may not be as elegant a way of doing this outside of simple fractions, which is the case with roman numerals. My guess is it might lend itself to a summed series of fractions with the denominator being the the Fibonacci series (instead of powers of 10). You want to use the right hand side though, flipping signs causes problems in infinite summed series. Another possibility is using the sets of the sequence so you have whole number + n/144 + j/144^2 + k/144^3 … similar to the algebraist system which has n/10 + j/100 + k/1000 …
Note: the start of the third series in the Fibonacci sequence is not exactly 144^2, but you get the idea.
Like decimals you would stop whenever you felt you had gone “far enough”. A more precise rule could be developed similar to the rules for determining the number of significant digits in the Arabist system.
Evaluation of Fibonacci numerals
Compared to Arabic you have to write more. In Arabic “4” is one digit and in this system, it is two. Likewise, 17 is two digits in Arabic, and three in this system. Thus, it is a little less efficient to write and speak. An obvious thing to do would be to make 4 (3+1) something that is easy to say, that is 3 and 1 said together contracts into a monosyllable, because it is a common re-occuring cause of an extra numeral.
The Fibonacci numeral system is better than Roman numerals in how many numerals are used. I would point out that Roman numerals were good enough to run a vast economy and produce many high-quality civil engineering works, but the difference in ease of use was noticeable enough the people did the hard job of switching to Arabic when it came along.
Compared to Binary (powers of 2 instead of 1.62), when written in string form it is a lot less compact because a lot of the information ‘space’ is not useable as you cannot have two x’s together, while you can have two 1s together in binary.
That a multiplication pattern can be followed is interesting and is a result of the powers pattern inherent in Fibonacci numerals. This means that multiplication by, say 3 can be rewritten as a number that is 1.62 to some power. With almost any other power this would get messy and off integers pretty quickly, but the beauty of the Fibonacci series is that this power is approximate and it always works out to integers. (At the cost of not precisely following the power rule.)
Matched to human lifecycle:
(Or why I picked 89 as the highest numeral in this system)
It occurs to me this number system matches life better in that a lot happens in childhood compared to adulthood and it corresponds to life events:
1 - learns basic movements
2 - toddler
3 - threenager
5 - A basic level of Independence, does not require constant monitoring.
8 - Age of accountability
13 - puberty
21 - full adulthood
34 - peak (Peak ages vary in different fields but this is about average. And in typical family formation mid-thirties is when adults would have the most dependents on them.)
55 - beginning of old age, beginning transition from caregiver to merely independent to needing care. (I.e. passing the torch phase.)
89 - death.
The above schema suggests a system of inheritance or passing on a business differing from primogeniture: your heir is a kid who is about 34 years younger than you. That way when you are 55 and just starting to slow down, you have an adult (21) looking for something to do with life and ready to start assuming responsibility. A smaller age gap means you are uncomfortably competitive with each other; a larger age gap risks the burden being dropped between encroaching frailness and youthfulness.