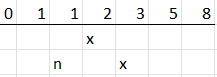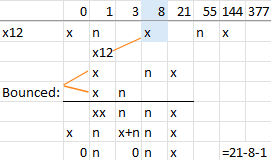After posting last Wednesday I’ve been thinking about all the dead information space on the Fibonacci string and wondering if there wasn’t same way to compress it, and perhaps a way that would still be easy to use and human compatible.
Review
The Fibonacci numeral system uses positive and negative numbers from the Fibonacci sequence to represent all number by adding them together. This is similar to Roman numerals and our number system where, for example, “34” means (3x10)+4. The Fibonacci number system has the problem that there are multiple ways of writing and saying the same number (roughly equivalent to saying eleventy-one instead of one hundred and eleven) such as 8+3 v. 13-3. I fixed it by introducing two rules which meant there is only one correct way of writing the number and also ensures that the least number of numerals are used to represent any number. The problem is that you get lots of dead information space when representing numerals as a string, which is useful for calculating in this system. XX is not allowed, X0X is not allowed (-x)0X is not allowed.
Solution: Every Other Numeral
Since every numeral is by definition of product of the two numerals before it, or the positive and negative numerals to either side of it, you can eliminate every other Fibonacci numeral by using the numerals to the side of it. 0X0→(-X)0X. Because of the rule set above, the spaces next to it will be empty. As an example, instead of writing the numeral ‘2’, we can write the numeral ‘-1’ and the numeral ‘3’, which together have the same value.
We eliminate every other position on the board and are left with 1, 3, 8, 21, 55. Let’s try counting to 8 see if this works
Looks pretty good. With three places we can count to 8. This is the same as binary. Except this is not binary, we can have three values in each location, +, -, or 0. This is trinary. Each location is not a bit (Binary Digit) but a Trinary Digit or trit.
3 trits have 3^3 (27) different configurations so with these numbers of trits we should be able to count all integers from -13 to 13.
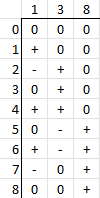
Lets try to count to 13.
We find that we can only count from -12 to 12 with three trits (by inverting the signs we get all the negatives). We are missing two spots. The trouble, as always in the Fibonacci numeral system, is 4 which can be represented with 1+3 and also 8-3-1. You can see that the count up is done differently from four to five in the above table. After 4 should be - - +, then 0 - +.
Still 25/27 percent efficiency is pretty good. A Fibonacci numeral civilization developing computation would certainly be tempted to go with that, and take the efficiency hit in exchange for the ease of converting between real life numbers and computer numbers, and once locked in it might not be worth it to convert back.
The actual trinary system has place values of 1, 3, 9 instead of 1, 3, 8. The value of the fourth trit would be 21 instead of 27, so we can assume the efficiency would go down with larger strings.
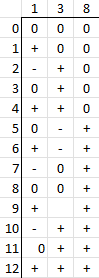
3 trits = -13 to 13 can do -12 to 12 so 93% of information space is useable.
4 trits = -40 to 40 can do -33 to 33. 83% of information space is useable.
5 trits = -121 to 121. Extrapolating that it will be the omitted Fibonacci numeral -1 (89-1=88, we can do -88 to 88. 73% of information space is used.
The problem with the dead space is not just that memory is not being used, its also that you can get these results as a sum or product and then there has to be another step to convert it to the correct format. Unless calculating in this format is a lot easier I’m guessing our Fibonacci computers are going to be abandoned.
Calculating with the Every Other Fibbonacci string.
Addition. As it turns out there are fewer rules for working with this compressed string.
An x and a (-x) in the same slot cancel each other out.
(“-x” will hereafter be represented by “n” for negative.)
Two x’s in the same spot lead are replaced with the string xnx. 0(2x)0 > xnx
In the full Fibonacci seqquence this looks like this: 00(2x)00 > xx(x)00 > x0(0)x0. The second x is on an omitted slot so it is replaced by an x one up and a n one down > x0(n)0x. The 0s are omitted numeral slots so they go away.
That’s it. That’s the whole ruleset. Since this already involves negatives, subtraction is already included. Rule #2 just inverts everything for negatives. Two ns in the same spot go to nxn. Above when I was counting in trinary and trying to puzzle out the rule, I was neglecting the potential for values to drop off into the zero slot and be discarded, which explains that seemingly bizarre exception.
Multiplication. Multiplication is simply addition repeated several times so applying the rules above we quickly find that the set patterns for each multiplication:
These product patterns are pleasingly symmetrical (easier to memorize). Here I am using 8 as the reference so these are all 8x?. But the pattern is the same just shifted so the blue origin is on what is being multiplied.
Like before the pattern ‘bounces’ off the zero, but now it is all negative on the bounce. 1x12 will show a good bounce:
Result is 21-8-1 or 12 as expected. However, the numbers are not what we expected which was 8+3+1. We still have some of the problem of the full set of numerals in that there are multiple ways to write things, and the simple rules account for it. Nothing obvious occurs to fix n0nx. In full Fibonacci it would n000n0x and the n0x would go to 0x0.
The computational rules aren’t simple like you’d want for computation, and for humans this system is poor because more numerals are needed to represent a number (8+3+1 instead of 13-1 for example). That creates more chances for error in calculations because you would have to apply the product pattern three times instead of two. Division would still be applying the negative of the product pattern, starting from the largest numeral, and repeating until cleared or the remaining number is lesser than the divisor.
Example 22 divided by 7
Other Compression Schemes:
I tried the numerals skipped, 1,2,5,13 &c. This worked out even worse.
Skipping double numerals leaves dead spots - numbers that can’t be represented by combinations of numerals.
Perhaps there is some merit in considering alternatives to a string of x, n, and 0. The calculations here are all based on an anchor point, the big end, the origin, perhaps working off the big numeral is the way to go. If I have as the big numeral 13, for example, I know I can’t have +/- 8 or +/-5, or -3, writing zeros in those spots is unneeded.